Answer:
1702.5
Explanation:
The n th term of an arithmetic progression is
 = a + (n - 1)d
= a + (n - 1)d
where a is the first term and d the common difference, hence
a + 5d = - 5 → (1) and
a + 9d = 21 → (2)
Subtract (1) from (2) term by term
4d = 26 ( divide both sides by 4 )
d =
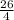 = 6.5 ← common difference
= 6.5 ← common difference
Substitute d = 6.5 into (1 )
a + 32.5 = - 5 ( subtract 32.5 from both sides )
a = - 37.5 ← first term
The sum to n terms of an arithmetic progression is
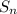 =
=
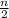 [ 2a + (n - 1)d ], hence
[ 2a + (n - 1)d ], hence
 = 15 [ - 75 + (29 × 6.5) ]
= 15 [ - 75 + (29 × 6.5) ]
= 15 [ - 75 + 188.5 ]
= 15 × 113.5
= 1702.5