Question

A crate with a mass of M = 62.5 kg is suspended by a rope from the endpoint of a uniform boom. The boom has a mass of m = 116 kg and a length of l = 7.65 m. The midpoint of the boom is supported by another rope which is horizontal and is attached to the wall as shown in the figure.

1. The boom makes an angle of θ = 57.7° with the vertical wall. Calculate the tension in the vertical rope.
2. What is the tension in the horizontal rope?

Answer 1

Tension in the vertical rope: approximately
`613 \; {\rm N}`.

Tension in the horizontal rope: approximately
`3.74 * 10^(3)\; {\rm N}`.

Assumption:
`g = 9.81\; {\rm N \cdot kg^(-1)}`.

Step-by-step explanation:

Since the system is not moving, the tension in the vertical rope would be equal to the weight of the crate:

`\begin{aligned}\text{weight of crate} &= m\, g \\ &= 62.5\; {\rm kg} * 9.81\; {\rm N \cdot kg^(-1)} \\ &= 613.25 \; {\rm N}\end{aligned}`.

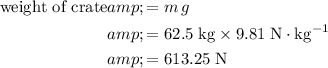Note that
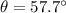`\theta = 57.7^(\circ)` is the angle between the beam (the lever) and the vertical rope. The torque that this vertical rope exert on the beam would be:

`\begin{aligned} \tau &= r\, F\, \sin(\theta) \\ &=(7.65\; {\rm m}) \, (613.25\; {\rm N})\, (\sin(57.7^(\circ))) \\ &\approx 3.965 * 10^(3)\; {\rm N \cdot m} \end{aligned}`.

This torque is in the clockwise direction.

The weight of the beam (
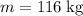`m = 116\; {\rm kg}`) would be:

`\begin{aligned}\text{weight of beam} &= m\, g \\ &= 116 \; {\rm kg} * 9.81\; {\rm N \cdot kg^(-1)} \\ &= 1.138 * 10^(3)\; {\rm N}\end{aligned}`.

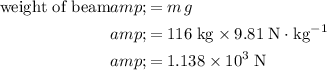Note that
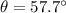`\theta = 57.7^(\circ)` is also the angle between the beam and the direction of the (downward) gravitational pull on this. Since this beam is uniform, it would appear as if the weight of this beam is applied at the center of this beam (with a distance of
`(7.65\; {\rm m}) / 2` from the pivot.) Thus, the torque gravitational pull exerts on this beam would be:

`\begin{aligned} \tau &= r\, F\, \sin(\theta) \\ &= \genfrac{(}{)}{}{}{7.65\; {\rm m}}{2} \, (1.138 * 10^(3)\; {\rm N})\, (\sin(57.7^(\circ))) \\ &\approx 3.679 * 10^(3)\; {\rm N \cdot m} \end{aligned}`.

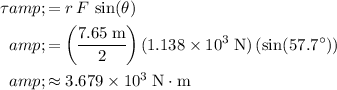This torque is also in the clockwise direction.

The tension in the horizontal rope would need to supply a torque in the counterclockwise direction. The magnitude of that torque would be approximately:

`\begin{aligned} & 3.965* 10^(3)\; {\rm N \cdot m} + 3.679* 10^(3)\; {\rm N \cdot m} \\ \approx \; & 7.645 * 10^(3)\; {\rm N \cdot m} \end{aligned}`.

Note the angle between the direction of this tension and the beam is
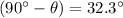`(90^(\circ) - \theta) = 32.3^(\circ)`. This force is applied
`(7.65\; {\rm m}) / 2` from the pivot. Hence, achieving that torque of
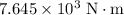`7.645 * 10^(3)\; {\rm N \cdot m}` would require:

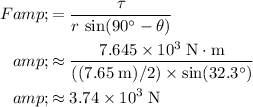`\begin{aligned} F &= (\tau)/(r\, \sin(90^(\circ) - \theta)) \\ &\approx \frac{7.645* 10^(3)\; {\rm N \cdot m}}{((7.65\; {\rm m}) / 2) * \sin(32.3^(\circ))} \\ &\approx 3.74 * 10^(3)\; {\rm N} \end{aligned}`.