Answers:
- Exponential and increasing
- Exponential and decreasing
- Linear and decreasing
- Linear and increasing
- Exponential and increasing
=========================================================
Step-by-step explanation:
Problems 1, 2, and 5 are exponential functions of the form
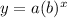where b is the base of the exponent and 'a' is the starting term (when x=0).
If 0 < b < 1, then the exponential function decreases or decays. Perhaps a classic example would be to study how a certain element decays into something else. The exponential curve goes downhill when moving to the right.
If b > 1, then we have exponential growth or increase. Population models could be one example; though keep in mind that there is a carrying capacity at some point. The exponential curve goes uphill when moving to the right.
In problems 1 and 5, we have b = 2 and b = 1.1 respectively. We can see b > 1 leads to exponential growth. I recommend making either a graph or table of values to see what's going on.
Meanwhile, problem 2 has b = 0.8 to represent exponential decay of 20%. It loses 20% of its value each time x increases by 1.
---------------------
Problems 3 and 4 are linear functions of the form y = mx+b
m = slope
b = y intercept
This b value is not to be confused with the previously mentioned b value used with exponential functions. They're two different things. Unfortunately letters tend to get reused.
If m is positive, then the linear function is said to be increasing. The line goes uphill when moving to the right.
On the other hand if m is negative, then we go downhill while moving to the right. This line is decreasing.
Problem 3 has a negative slope, so it is decreasing. Problem 4 has a positive slope which is increasing.