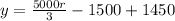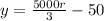Question

2.3.2: Michael Myers predicts that SAT scores predict college graduation rates in a linear fashion. U of M has an average SAT of 1450 and a graduation rate of 90%. GVSU has an average SAT of 1110 and a graduation rate of 69.6%. Write an equation to represent the linear relationship . Be sure your equation is in slope-intercept form

Answer 1

`y = (5000r)/(3) -50`

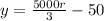
Explanation:

Represent the SAT score with y and the rate with r.

So, we have:

`(r_1,y_1) = (90\%,1450)`

`(r_2,y_2) = (69.6\%,1110)`

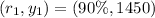
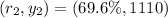
Required

Determine the equation in slope intercept form

First, we calculate the slope

`m =(y_2 - y_1)/(r_2 - r_1)`

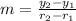
This gives:

`m =(1110 - 1450)/(69.6\% - 90\%)`

`m =(-340)/(-20.4\%)`

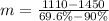
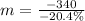
Convert percentage to decimal

`m =(-340)/(-0.204)`

`m =(340)/(0.204)`

Multiply by 1000/1000

`m =(340*1000)/(0.204*1000)`

`m =(340000)/(204)`

`m = (5000)/(3)`

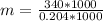
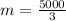
The equation is then calculated as:

`y - y_1 = m(r - r_1)`

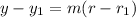
This gives:

`y - 1450 = (5000)/(3)(r - 90\%)`

Open Bracket

`y - 1450 = (5000r)/(3) - (5000)/(3)*90\%`

Convert percentage to decimal

`y - 1450 = (5000r)/(3) - (5000)/(3)*0.90`

`y - 1450 = (5000r)/(3) - 5000*0.30`

`y - 1450 = (5000r)/(3) - 1500`

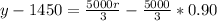
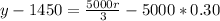
Make y the subject

`y = (5000r)/(3) - 1500+1450`

`y = (5000r)/(3) -50`