Answer:
W = 10 cm
Explanation:
Area of a Triangle and a Rectangle
The area of a triangle of base B and height H is:
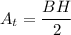
The area of a rectangle of width W and length L is:

We are given the base of the triangle B=6 cm and the height H=8 cm, thus the area is:
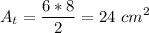
The area of the rectangle is 5 times the area of the triangle, thus:
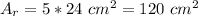
If we know the area of the rectangle and its length, we can find the width by solving for W:
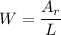
The rectangle has a length of L=12 cm, thus:
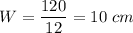
W = 10 cm