Question

Given f(x)=2x2−5x−3 and g(x)=2x2+x .

What is (fg)(x) ?





−2x−3x where x≠0, −12


x−3x where x≠0, −12


x−2x−3 where x≠0, −32


xx−3 where x≠0, 3

Answer 1

(fg)(x) =
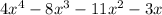`4x^(4)-8x^(3)-11x^(2)-3x` is the answer.

Explanation:

It is given f(x) = 2x² - 5x -3 and g(x) = 2x² + x

Then we have to find (fg)(x)

As we know (fg)(x) = f(x).g(x)

By putting the values of f(x) and g(x)

(fg)(x) = (2x² - 5x - 3)(2x²+x)

= 2x²(2x²+x) - 5x(2x² + x) - 3(2x² + x)

=
`4x^(4)+2x^(3)-10x^(3)-5x^(2)-6x^(2)-3x`

=
`4x^(4)-8x^(3)-11x^(2)-3x`

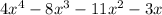
So the value of (fg)(x) =
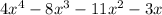`4x^(4)-8x^(3)-11x^(2)-3x` is the answer.

Answer 2

For (fg)(x)

(fg) (x) = 4x^4 - 8x^3 -11x^2 -3x

With no restrictions on the x

Explanation:

To find (fg) (x) = f(x) . g(x)

We need to multiply f(x) with g(x)

(fg) (x) = (2x^2 -5x -3) * (2x^2 + x)

fg(x) = 4x^4 + 2x^3 - 10x^3 - 5x^2 -6x^2 -3x

fg(x) = 4x^4 - 8x^3 -11x^2 -3x