With
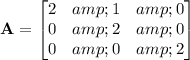
we have
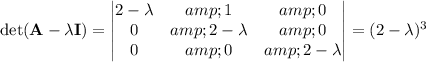
so
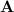 has one eigenvalue,
has one eigenvalue,
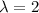 , with multiplicity 3.
, with multiplicity 3.
In order for
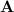 to not be defective, we need the dimension of the eigenspace to match the multiplicity of the repeated eigenvalue 2. But
to not be defective, we need the dimension of the eigenspace to match the multiplicity of the repeated eigenvalue 2. But
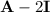 has nullspace of dimension 2, since
has nullspace of dimension 2, since
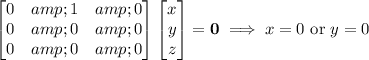
That is, we can only obtain 2 eigenvectors,

and there is no other. We needed 3 in order to complete the basis of eigenvectors.