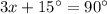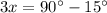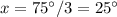Answer:
Part 1)
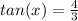
Part 2)

Part 3)
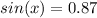
Part 4)

Explanation:
Part 1) Note In this problem sinx should be 4/5 not 45 and cosx should be 3/5 not 35
Given sinx=4/5 and cosx=3/5 (see the note)
What is ratio for tanx ?
we know that

substitute the values
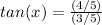
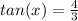
Part 2) ∠A is an acute angle in a right triangle
Note In this problem cosA should be 15/17 not 1517
Given that cosA=15/17, what is the ratio for sinA?
we know that
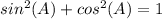
substitute the value of cos(A) and solve for sin(A)


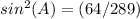

Part 3) Given sinx=0.5 , what is cosx ?
we know that
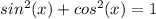
substitute the value of sin(x) and solve for cos(x)
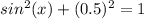
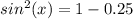
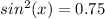
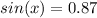
Part 4) What is the value of x?
sin(x+22)°=cos(2x−7)°
we know that
if
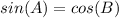
then
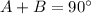 -----> by complementary angles
-----> by complementary angles
so
in this problem
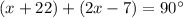
solve for x