Question

Eric took out an 80/20 mortgage to buy a house costing $175,000. The first (80%) mortgage has an interest rate of 4.75%, and the second (20%) mortgage has an interest rate of 7.525%. Both are 30-year fixed-rate mortgages. What is total mortgage payment for this house?

A. $975.63

B. $805.87

C. $245.32

D. $730.31

Answer 1

Answer:975.63

Explanation:

Answer 2

The total monthly mortgage payment for the house is $975.63

Explanation:

The principle amount is $175000

80% of 175000 is =
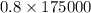`0.8*175000` = $140000

20% of 175000 is =
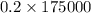`0.2*175000` = $35000

Emi formula is :

`(p* r*(1+r)^(n) )/((1+r)^(n)-1 )`

For 1st part:

p = 140000

r = 4.75/12/100=0.00395

n =
`30*12=360`

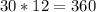
Putting values in formula we get

`(140000*0.00395*(1.00395)^(360) )/((1.00395)^(360)-1 )`

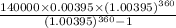
= $729.508

For 2nd part:

p = 35000

r = 7.525/12/100=0.00627

n =
`30*12=360`

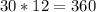
Putting values in formula we get

`(35000*0.00627*(1.00627)^(360) )/((1.00627)^(360)-1 )`

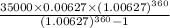
= $245.301

Adding both the monthly payments:

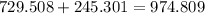`729.508+245.301=974.809` dollars

This is closest to option A.

So, option A is the answer.

And for 30 years the mortgage payment will be =

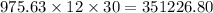`975.63*12*30=351226.80` dollars