Answer:
12.22 cm
Explanation:
We'll be using cosine laws to solve for QR side:
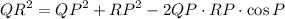
We know that QP = 13 cm, RP = 4 cm and cosP = 70°. Hence:

Then evaluate the expression:
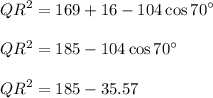
Square root both sides, since length can only be positive. The negative side will be cancelled:
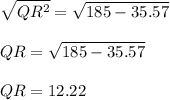
Therefore, the length of QR will be around 12.22 cm or 12 cm when rounded to nearest integer.