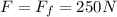Question

If you pull horizontally on a desk with a force of 150 N and the desk doesn't move, the friction force must be 150 N. Now if you pull with 250 N so the desk slides at constant velocity, the friction force is

Answer 1

The friction force is 250 N

Step-by-step explanation:

The desk is moving at constant velocity. This means that its acceleration is zero: a = 0. Newton's second law states that the resultant of the forces acting on the desk is equal to the product between mass (m) and acceleration (a):

`\sum F=ma`

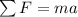
In this case, we know that the acceleration is zero: a = 0, so also the resultant of the forces must be zero:

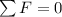`\sum F = 0` (1)

We are only interested in the forces acting along the horizontal direction, since it is the direction of motion. There are two forces acting in this direction:

- the pull, forward, F = 250 N

- the friction force, backward,
`F_f`

Given (1), we have

`F-F_f = 0`

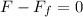
So the force of friction must be equal to the pull:

`F=F_f = 250 N`