Question

Without graphing, what are the vertex , axis of symmetry, and transformations of the parent function? Y - |8x-3| - 3

Answer 1

Given:

Consider the given function is

`y=|8x-3|-3`

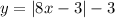
To find:

The vertex , axis of symmetry, and transformations of the parent function?

Solution:

We have,

`y=|8x-3|-3`

`y=\left|8\left(x-(3)/(8)\right)\right|-3`

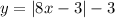
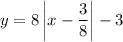`y=8\left|x-(3)/(8)\right|-3` ...(i)

It is an absolute function.

The vertex form of an absolute function is

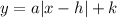`y=a|x-h|+k` ...(ii)

where, a is a constant, (h,k) is vertex and x=h is axis of symmetry.

From (i) and (ii), we get

`a=8,h=(3)/(8),k=-3`

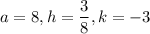
So,

`\text{Vertex}:(h,k)=\left((3)/(8),-3\right)`

`\text{Axis of symmetry}:x=(3)/(8)`

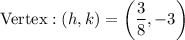
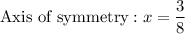
Parent function of an absolute function is

`y=|x|`

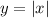
Since, a=8 therefore, parent function vertically stretched by factor 8.

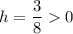`h=(3)/(8)>0`, so the function shifts
`(3)/(8)` unit right.

k=-3<0, so the function shifts 3 units down.

Therefore, the vertex is
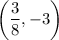`\left((3)/(8),-3\right)` and Axis of symmetry is
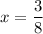`x=(3)/(8)`. The parent function vertically stretched by factor 8, shifts
`(3)/(8)` unit right and 3 units down.