Answer:
i)D:
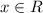
ii)R:
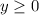
iii) Y-int:(0,3)
Explanation:
i) The given absolute value function is;
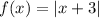 .
.
The absolute value function is defined for all real values of x.
The domain is all real numbers.
ii) The range is all y-values that will make x defined.
The given function,
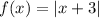 .
.
has vertex at, (-3,0) and opens upwards.
This implies that, the minimum y-value is 0.
The range is
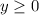
iii) To find the y-intercept substitute x=0 in to the function.
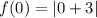 .
.
 .
.
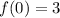 .
.
The y-intercept is (0,3)
See attachment for graph.