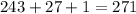Question

How many five digit palindromes are there where the digit “1” appears at least once?

Answer 1

A 5 digit palindrome number must be written as

`xyzyx`

where
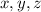`x, y, z` are digits. We want "1" to appear at least once, which leads to the following cases:

Only one of the variable is equal to 1 (the other two are not)

In this case, the possible patterns of the numbers are
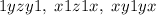`1yzy1,\ x1z1x,\ xy1yx`. We have 9 choices for each of the non-one digits (all the reamaining digits). So, the count of these kind of number is

`(9\cdot 9)\cdot 3 = 243`

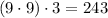
Two variables are equal to 1 (the third is not)

In this case, the possible patterns of the numbers are
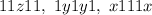`11z11,\ 1y1y1,\ x111x`. We have 9 choices for the non-one digit (all the reamaining digits). So, the count of these kind of number is

`9\cdot 3 = 27`

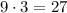
All variables are equal to 1

In this trivial case we only have one number,
`11111`

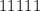
Total:
`243+27+1 = 271`