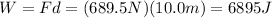Question

A cave rescue team lifts an injured spelunker directly upward and out of a sinkhole by means of a motor-driven cable. The lift is performed in three stages, each requiring a vertical distance of 10.0 m. (1) First, the initially stationary spelunker is accelerated to a speed of 4.40 m/s. (2) Then he is then lifted at the constant speed of 4.40 m/s. (3) Finally he is decelerated to zero speed. How much work is done on the 78.0 kg rescuee by the force lifting him during each stage? Work done on rescuee during stage (1) kJ Work done on rescuee during stage (2) kJ Work done on rescuee during stage (3) kJ

Answer 1

(1) 8408 J = 8.4 kJ

We need to find the acceleration of the spelunker first, through the equation:

`v^2-u^2=2ad`

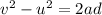
where

v = 4.40 m/s is the final speed

u = 0 is the initial speed

a is the acceleration

d = 10.0 m is the distance

Solving the equation for a, we find

`a=(v^2-u^2)/(2d)=((4.40 m/s)^2-0)/(2(10.0 m))=0.97 m/s^2`

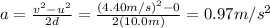
In order to find the magnitude of force F used to lift the spelunker, we have to apply Newton's second law:

`\sum F = ma\\F - mg = ma`

where (mg) is the weight of the spelunker, and a = 0.97 m/s^2. Solving for F, we find

`F=m(g+a)=(78.0 kg)(9.81 m/s^2+0.97 m/s^2)=840.8 N`

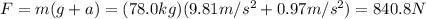
And so, the work done by the force during this stage is

`W=Fd=(840.8 N)(10.0 m)=8408 J`

(2) 7644 J = 7.6 kJ

The work done on the spelunker in this stage is

`W=Fd`

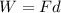
where F is the force applied on the spelunker to lift him, and d = 10.0 m is the vertical distance through which the spelunker is lifted.

In order to find the magnitude of F, we have to apply Newton's second law:

`\sum F = ma\\F - mg = ma`

where (mg) is the weight of the spelunker, and the acceleration is zero because he is moving at constant speed: so, a=0, and the equation becomes

`F-mg=0\\F=mg=(78.0 kg)(9.8 m/s^2)=764.4 N`

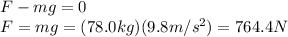
So, the work done is

`W=(764.4 N)(10.0 m)=7644 J`

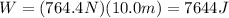
3) 6895 J = 6.9 kJ

This stage is similar to stage (1); we find the deceleration using:

`v^2-u^2=2ad`

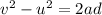
where

v = 0 m/s is the final speed

u = 4.40 is the initial speed

a is the acceleration

d = 10.0 m is the distance

Solving the equation for a, we find

`a=(v^2-u^2)/(2d)=(0-(4.40 m/s)^2)/(2(10.0 m))=-0.97 m/s^2`

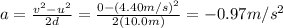
In order to find the magnitude of force F used to lift the spelunker, we have to apply Newton's second law:

`\sum F = ma\\F - mg = ma`

where (mg) is the weight of the spelunker, and a = -0.97 m/s^2. Solving for F, we find

`F=m(g+a)=(78.0 kg)(9.81 m/s^2-0.97 m/s^2)=689.5 N`

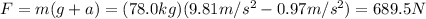
And so, the work done by the force during this stage is

`W=Fd=(689.5 N)(10.0 m)=6895 J`