Question

2. Find the 20th term of an arithmetic sequence if its 6th term is 14 and 14th term is 6.

can anyone answer this ?​

Answer 1

0

Explanation:

The number of terms of an Arithmetic progressions has the formular.

Tn = a + ( n - 1 ) d

From the question,

6th term = 14

14th term = 6

Therefore,

a + 5d = 14 -----------(1)

a + 13d = 6 ----------(2)

subtracting

-8d = 8

dividing bothsides by -8

`( - 8d)/( - 8) = (8)/( - 8) \\ d = - 1`

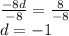
Therefore,

common difference= -1

substituting the value of d into equation (1)

a + 5 ( -1) = 14

a - 5 = 14

a = 14 + 5 = 19

First term = 19

For the 20th term

T 20 = a + 19d

19 + 19 ( -1 )

19-19 = 0

Therefore,

20th term = 0

Answer 2

`\sf t_(20)= 0`

Explanation:

Arithmetic sequence:

`\sf \boxed{\bf n^(th) \ term = a + (n-1)d}\\\\\text{Here, a is the first term ; d is the common difference }`

6th term is 14 ⇒
`\sf t_6 = 14`

a + (6 - 1)d = 14

a + 5d = 14 --------------(I)

14th term is 6 ⇒
`\sf t_(14) = 6`

a + (14-1)d = 6

a + 13d = 6 ----------------(II)

Subtract equation (II) from equation(I)

(I) a + 5d = 14

(II) a + 13d = 6

- - -

-8d = 8

d = 8 ÷(-8)

`\sf \boxed{\bf d= (-1)}`

Plugin d = -1 in equation (I)

a + 5(-1) = 14

a -5 = 14

a = 14 + 5

`\sf \boxed{\bf a = 19}`

20th term:

`\sf t_(20)= 19 + 19*(-1)`

= 19 - 19

`\sf \boxed{\bf t_(20) = 0}`