The first system of equations,
 and
and
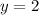 , has no real number solutions.Therefore, option A is correct
, has no real number solutions.Therefore, option A is correct
The question asks which systems of equations have no real number solutions. To determine this, we can set the quadratic equation equal to the linear equation and look at the discriminant of the resulting quadratic equation. The discriminant,
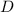 , is found from the standard quadratic equation
, is found from the standard quadratic equation
 and is given by
and is given by
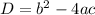 .
.
If
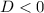 , the quadratic equation has no real solutions.
, the quadratic equation has no real solutions.
Let's go through each system and apply this:
1.
 and
and
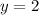
Substitute
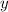 from the second equation into the first:
from the second equation into the first:
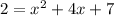
The quadratic equation becomes
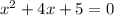
Here,
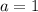 ,
,
 , and
, and
 .
.
Calculate the discriminant
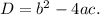
2.
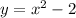 and
and

Substitute
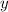 from the second equation into the first:
from the second equation into the first:
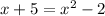
The quadratic equation becomes

Here,
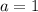 ,
,
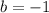 , and
, and

Calculate the discriminant
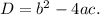
3.
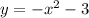 and
and
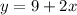
Substitute \( y \) from the second equation into the first:
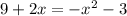
The quadratic equation becomes
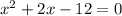
Here,
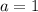 ,
,
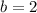 , and
, and
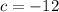 .
.
Calculate the discriminant
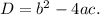
4.
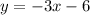 and
and
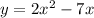
Substitute
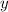 from the second equation into the first:
from the second equation into the first:
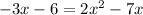
The quadratic equation becomes \( 2x^2 - 4x - 6 = 0 \)
Here,
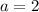 ,
,
 , and
, and
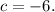
Calculate the discriminant
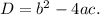
5.
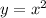 and
and
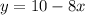
Substitute \( y \) from the second equation into the first:
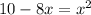
The quadratic equation becomes
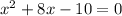
Here,
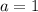 ,
,
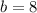 , and
, and

Calculate the discriminant
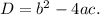
Now we'll calculate the discriminant for each and determine if any are less than zero.
After calculating the discriminant for each system of equations:
1. For the system
 and
and
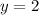 , the discriminant is
, the discriminant is
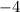 . Since the discriminant is less than zero, this system has no real number solutions.
. Since the discriminant is less than zero, this system has no real number solutions.
2. For the system
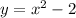 and
and
 , the discriminant is
, the discriminant is
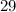 . Since the discriminant is greater than zero, this system has real number solutions.
. Since the discriminant is greater than zero, this system has real number solutions.
3. For the system
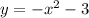 and
and
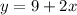 , the discriminant is
, the discriminant is
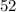 . Since the discriminant is greater than zero, this system has real number solutions.
. Since the discriminant is greater than zero, this system has real number solutions.
4. For the system
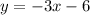 and
and
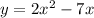 , the discriminant is
, the discriminant is
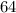 . Since the discriminant is greater than zero, this system has real number solutions.
. Since the discriminant is greater than zero, this system has real number solutions.
5. For the system
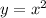 and
and
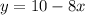 , the discriminant is
, the discriminant is
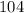 . Since the discriminant is greater than zero, this system has real number solutions.
. Since the discriminant is greater than zero, this system has real number solutions.
Therefore, only the first system of equations,
 and
and
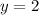 , has no real number solutions.
, has no real number solutions.