Answer:
Option B is correct.
Explanation:
Given that Travis wants to solve a quadratic equation. Since his equation cannot be factored, Travis has to graph the equation and approximate the solution(s).
we have to find the equation that Travis is trying to solve.
The equation which Travis trying to solve can't be factored therefore we have to find the equation which can't be factored i.e whose determinant is non-perfect square

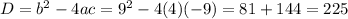
which is a perfect square.
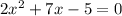
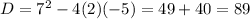
which is not a perfect square.
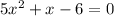
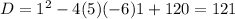
which is a perfect square.

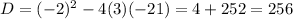
which is a perfect square.
Hence, the only equation whose discriminant is not a perfect square i.e the only equation which can't be factored is
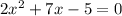
∴ Option B is correct.