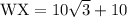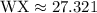Question

What is WX? Explain your reasoning.

I know all the angles but I’m not sure on how to find WX or what equation to use.

Answer 1

180

Explanation:

Solution 1: Any straight line is 180 degrees.

Solution 2: Angle WX=Angle YZW+ Angle YZX

Angle YZW=Angle YZX=90

Angle YZW+ Angle YZX=90+90=180

So Angle WX=180

Answer 2

Explanation:

You can find WX if you know some special properties of special triangles:

1. A 45-45-90 triangle (a triangle with angle measures of 45°, 45°, and 90°) will have a 1:1:√2 ratio (the legs of the triangle are the same length and the hypotenuse is the length of any leg times √2)

2. A 30-60-90 triangle (a triangle with angle measures of 30°, 60°, and 90°) will have a 1:√3:2 ratio (the hypotenuse is twice the measure of the shorter leg, and the longer leg is √3 times the length of the shorter leg)

For reference, a leg is a side on a right triangle that isn't the hypotenuse.

In this picture, the first type of triangle is on the right, and the second type is on the left.

WZ

The shorter leg on the left triangle has a length of 10, and WZ is the longer leg. The longer leg is √3 times the shorter one, so WZ = 10√3

ZX

Both legs of a 45-45-90 triangle have the same measure, so ZX is 10.

Since WX is made up of WZ and ZX, it's length is the sum of both lengths.

`{\rm WX} = 10√(3)+10`

`{\rm WX} \approx 27.321`