Question

The side of a square measures (3x − 6) units. Part A: What is the expression that represents the area of the square? Show your work to receive full credit. (4 points) Part B: What are the degree and classification of the expression obtained in Part A? (3 points) Part C: How does Part A demonstrate the closure property for polynomials? (3 points)

Answer 1

See below.

Explanation:

A. the area is the square of the length of a side.

Area = (3x - 6)^2

= 9x^2 - 18x - 18x + 36

= 9x^2 - 36x + 36 (answer).

B. The above answer is a polynomial (trinomial) , degree 2.

C. It demonstrates that when we multiply 2 polynomials the answer is also a polynomial.

Answer 2

Answer: A)
`(3x-6)^2=9x^2-36x+36`

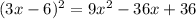
B) Degree - 2

Classification - Quadratic equation

C) Multiplication of two polynomials is always a polynomial.

Explanation:

Since we have given that

Side of a square = (3x-6) units

We need to find the area of square.

As we know the formula for area of square:

Part A: Area of square is given by

`Side^2=(3x-6)^2=9x^2-36x+36`

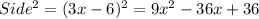
Part B : Degree of the expression obtained in the first part is 2.

Classification of the expression - Quadratic equation.

Part C: Multiplication of two polynomials is always a polynomial.