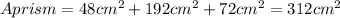Answer: OPTION B
Explanation:
Calculate the area the triangles (Both are equal, then you can multiply the area of one of them by 2):
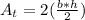
Where b is the base and h is the height:
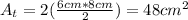
Calculate the area of the rectangles that are equal (you can multiply the area of one of them by 2):
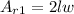
Where l is the length and w is the width:

Calculate the area of the other rectangle:
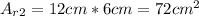
Add the areas. Then, the result is: