Answer:
The solution of the system of equations are the points (-2,-6) and (4,6)
Explanation:
we have
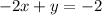 ----> equation A
----> equation A
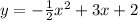 ----> inequality B
----> inequality B
we know that
The solution of the system of equations is the intersection point both graphs
To graph the linear equation, find the intercepts
Find the y-intercept
The y-intercept is the value of y when the value of x is equal to zero
For x=0
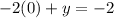
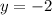
The y-intercept is the point (0,-2)
Find the x-intercept
The x-intercept is the value of x when the value of y is equal to zero
For y=0
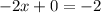

The x-intercept is the point (1,0)
Plot the intercepts to graph the linear equation and find the intersection points with the quadratic equation
The intersection points are (-2,-6) and (4,6)
see the attached figure
therefore
The solution of the system of equations are the points (-2,-6) and (4,6)