Question

Which of these shows how the formulas for the area of a circle and the volume of a cylinder are related? A. The area of a circle provides the radius of the cylinder’s base. Dividing that by the surface area of the cylinder’s base adds the third dimension of the solid. B. The area of a circle provides the height of the cylinder. Multiplying that by the surface area of the cylinder’s base adds the third dimension of the solid. C. The area of a circle provides the surface area of a cylinder’s base. Multiplying that by the height of the cylinder adds the third dimension of the solid.

Answer 1

Answer: OPTION C.

Explanation:

The area of a circle can be calculated with the following formula:

`A=r^2\pi`

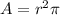
Where r is the radius.

The base of a cylinder (which is a 3-dimensional solid) is a circle, then the surface area of the base can be calculated with
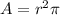`A=r^2\pi`. When the surface area of the base is multiplied by the height of the cylinder, you obtain the volume ( Then the third dimension of the solid is added):

`V=hr^2\pi`

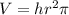
Where h is the height and r is the radius.

Therefore the answer is: C. The area of a circle provides the surface area of a cylinder’s base. Multiplying that by the height of the cylinder adds the third dimension of the solid.