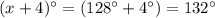Question

N a heptagon, the degree measures of the interior angles are $x, ~x, ~x-2, ~x-2,

~x + 2, ~x + 2$ and $x + 4$ degrees. What is the degree measure of the largest interior angle?

Answer 1

Answer:132°

Explanation:

Answer 2

The measure of the largest interior angle is
`132\°`

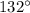
Explanation:

we know that

The sum of the interior angles in a polygon is equal to the formula

`S=(n-2)180\°`

where

n is the number of sides of polygon

In this problem we have a heptagon

so

`n=7\ sides`

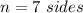
substitute the value in the formula

`S=(7-2)180\°=900\°`

`S=x+x+(x-2)+(x-2)+(x+2)+(x+2)+(x+4)`

`900=x+x+(x-2)+(x-2)+(x+2)+(x+2)+(x+4)`

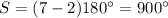
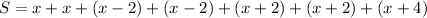
Solve for x

`900=7x+4`

`7x=900-4`

`7x=896`

`x=128\°`

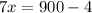
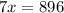
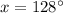
Find the measure of the largest interior angle

`(x+4)\°=(128\°+4\°)=132\°`