Question

A solution of benzene (C6H6) and toluene (C7H8) is 25.0% benzene by mass. The vapor pressures of pure benzene and pure toluene at 25°C are 94.2 torr and 28.4 torr, respectively. Assuming ideal behavior, calculate the following: (a) the vapor pressure of each solution component in the mixture (b) the total pressure above the solution (c) the composition of the vapor in mass percent Why is the composition of the vapor different from the composition of the solution?

Answer 1

(a) The vapor pressure of each solution component in the mixture.

Raoult's law states that the partial vapor pressure of each component of an ideal liquid mixture is equal to the vapor pressure of the pure component multiplied by its molar fraction in the mixture. Mathematically, Raoult's law is expressed as,

`P_(j) = x_(j) P^(*) _(j)`

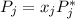
where
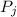`P_(j)` is the partial pressure of component j in the gas mixture above the solution,
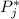`P^(*)_(j)` is the vapor pressure of the pure component and
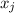`x_(j)` is the molar fraction of component j in the liquid mixture (in the solution).

To find the vapor pressures of benzene and toluene we must first calculate their molar fractions in the solution. If we consider 100.0 g of solution then we will have 25.0 g of benzene and 75.0 g of toluene (because 100.0 g - 25.0 g = 75.0 g) in the mixture. In this way, the number of moles of each component in the solution will be,

`n_(benzene) = 25.0 g x (1 mol)/(78.11 g) = 0.320 mol`

`n_(toluene) = 75.0 g x (1 mol)/(92.14 g) = 0.814 mol`

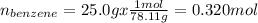
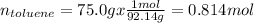
Then, the molar fractions of each component will be,

`x_(benzene) = (n_(benzene) )/(n_(total) ) = (0.320 mol)/(0.320 mol + 0.814 mol)` →
`x_(benzene) = 0.28`

`x_(toluene) = 1 - x_(benzene)` →
`x_(toluene) = 0.72`

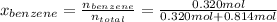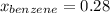
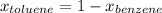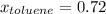
If the vapor pressures of pure benzene and pure toluene at 25°C are 94.2 torr and 28.4 torr, respectively, according to Raoult's law,

`P_(benzene) = x_(benzene) P^(*) _(benzene) = 0.28 x 94.2 torr`

→
`P_(benzene) = 26.4 torr`

`P_(toluene) = x_(toluene) P^(*) _(toluene) = 0.72 x 28.4 torr`

→
`P_(toluene) = 20.5 torr`

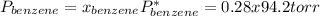
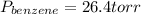
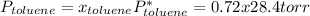
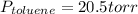
So, the vapor pressures of benzene and toluene in the mixture are 26.4 torr and 20.5 torr, respectively.

(b) The total pressure above the solution.

The law of partial pressures, known as Dalton's law, states that the pressure of a mixture of gases, which do not react chemically and behave like ideal gases, is equal to the sum of the partial pressures that each of them exerts if only one occupied the entire volume of the mixture, without changing the temperature.

In this way, in the mixture in question, according to the Dalton's law, the total pressure will be,

`P_(total) = P_(benzene) + P_(toluene)  = 26.4 torr + 20.5 torr`

→
`P_(total) = 46.9 torr`

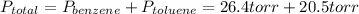
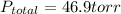
So, the total pressure above the solution is 46.9 torr.

(c) The composition of the vapor in mass percent.

According to Dalton's law,

`P_(j) = y_(j) P_(total)`

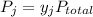
where
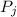`P_(j)` is the partial pressure of the gas j,
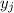`y_(j)` is the mole fraction of the gas j in the gas mixture and
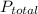`P_(total)` is the total pressure.

To know the composition of the vapor we must first calculate the molar fractions of the components of the mixture in the vapor:

`y_(benzene) = (P_(benzene) )/(P_(total) ) = (26.4 torr)/(46.9 torr)`

→
`y_(total) = 0.56`

`y_(toluene) = 1 - y_(benzene)` →
`y_(toluene) = 0.44`

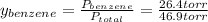
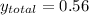
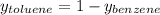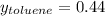
If we consider 1 mole of solution then we will have 0.56 mol of benzene and 0.44 mol of toluene in the vapor. In this way, the number of grams of each component in the vapor will be,

`g_(benzene) = 0.56 mol x (78.11 g)/(1 mol) = 43.7 g`

`g_(toluene) = 0.44 mol x (92.14 g)/(1 mol) = 40.6 g`

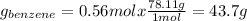
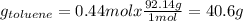
The percentage by mass of each component in the vapor will be,

% benzene = (g benzene / g total) x 100% = (43.7 g / (43.7 g + 40.6 g)) x 100% → % benzene = 51.8 %

% toluene = 100 % - % benzene → % toluene = 41.2%

So, the composition of the vapor in mass percent is 51.8 % benzene and 41.2% toluene.

Why is the composition of the vapor different from the composition of the solution?

The composition of the vapor will be different from that of the solution, since the more volatile compound will have a larger molar fraction in the vapor phase than in the liquid phase.

In a mixture with different volatile components the compound that volatilizes more easily is the one that will have greater capacity to escape from the solution in the form of vapor and, therefore, will be in a greater composition in the vapor above the solution.

We can measure this by means of vapor pressure, which is a measure of the volatility of a substance, that is, the capacity of the substance to pass from a liquid to a gaseous state. In the question, benzene is in greater proportion than toluene in the vapor mixture since it has a higher vapor pressure (94.2 torr) than toluene (28.4 torr).