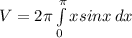Answer:
See attached picture.
Explanation:
The idea of the shell method is to find the volume of a differential shell by using the formula:
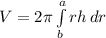
in the drawing we can see that r=x, h=sin x and dr=dx. The area is revolving about the y-axis from x=0 to
 . So the volume is found by using the following integral:
. So the volume is found by using the following integral: