A periodic wave can be written as:

where
A is the amplitude, k is the wave number, x is the position,
 is the angular frequency and t is the time.
is the angular frequency and t is the time.
1. A represents the amplitude
Explanation: the term A inside the wave equation represents the amplitude, which is the maximum displacement of the wave (along the y-axis) with respect to tis equilibrium position. Basically, when the sine part of the wave is equal to 1, y=A, and the wave has the maximum displacement.
2. Wavelength
Explanation: the wavelength of a wave is defined as the distance between two successive crests (or between succesive throughs) of the wave.
The wavelength (indicated with
 ) is related to the wave number, k, by the equation
) is related to the wave number, k, by the equation
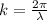
3.
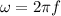
The frequency at which the source of the wave is oscillating, f, is related to the angular frequency
 by the relationship
by the relationship
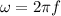
basically, f expresses the frequency in units of Hertz (1/s), while the angular frequency expresses the frequency in units of radians per second.
4.
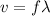
The relationship between wave speed, wave frequency and wavelength is
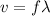
where
v is the wave speed
f is the frequency
 is the wavelength
is the wavelength
We can observed that if the speed of the wave is constant, then the frequency and the wavelength are inversely proportional to each other.