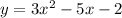Answer:
Explanation:
Let the quadratic function be

The given points must satisfy this function;
Substitute
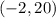 .
.
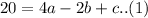
Substitute (0,-2)
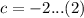
Substitute (1,-4);
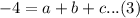
Put equation (2) into equation (1)
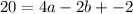
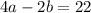
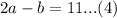
Put equation (2) into equation (3)
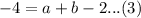
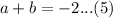
Add equation (4) and (5)
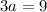
Divide both sides by 3
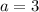
Put a=3 in equation 5.
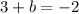

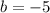
The quadratic function is;