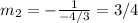Question

What is the slope of a line that is perpendicular to the line shown.

Answer options: 2/3, 3/4, -3/4, -4/3.

Answer 1

3/4

Explanation:

First of all, we need to calculate the slope of the line shown. This can be computed as:

`m=(\Delta y)/(\Delta x)`

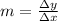
where

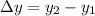`\Delta y = y_2-y_1` is the increment along the y-direction

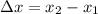`\Delta x = x_2 - x_1` is the increment along the x-direction

We can choose the following two points to calculate the slope of the line shown:

(-3,2) and (0,-2)

And so, the slope of the line shown is

`m=(-2-(2))/(0-(-3))=-(4)/(3)`

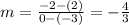
Two lines are said to be perpendicular if the slope of the first line is the negative reciprocal of the slope of the second line:

`m_2 = -(1)/(m_1)`

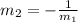
Using
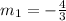`m_1 = -(4)/(3)`, we find that a line perpendicular to the line shown should have a slope of

`m_2 = -(1)/(-4/3)=3/4`