Question

SOMEONE PLEASE HELP ME ASAP, PLEASE!!

There are 24 students in Mrs. Noether's third grade class, and there are 3 books on the reading list for book reports this quarter. Mrs. Noether wants to assign 8 students to Book A, 10 students to Book B, and 6 students to Book C. How many distinct ways can she do this?

This is a combination problem with grouping.

Answer 1

The number of distinct ways she can do this is:

6635520 ways

Explanation:

If we have to chose r items out of a total of n items then the number of ways of doing so is given by:

`n_C_r=(n!)/(r!* (n-r)!)`

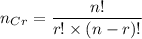
There are 24 students in Mrs. Noether's third grade class.

Now, Mrs. Noether wants to assign 8 students to Book A.

This means that the number of ways of doing so is:

`{24}_C_(8)`

10 students are to be assigned to Book B.

The number of ways of doing so is:

`{24}_C_(10)`

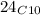
and 6 students to Book C.

The number of ways of doing so is:

`{24}_C_(6)`

Hence, the total number of distinct ways of doing so is:

`{24}_C_(8)* {24}_C_(10)* {24}_C_(6)`

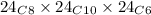
which on solving gives:

6635520 ways