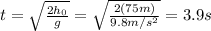a) 70.1 m
The ball is moving by uniformly accelerated motion, with constant acceleration
 (acceleration due to gravity) towards the ground. The height of the ball at time t is given by the equation
(acceleration due to gravity) towards the ground. The height of the ball at time t is given by the equation
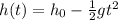
where
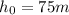 is the height of the ball at time t=0. Substituting t=1 s, we can find the height of the ball 1 seconds after it has been dropped:
is the height of the ball at time t=0. Substituting t=1 s, we can find the height of the ball 1 seconds after it has been dropped:
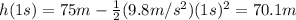
b) 3.9 s
We can still use the same equation we used in the previous part of the problem:
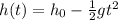
This time, we want to find the time t at which the ball hits the ground, which means the time t at which h(t)=0. So we have

And solving for t we find