Answer:
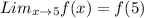 .
.
Explanation:
The given function is
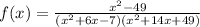 .
.
We can factor an rewrite for easy evaluation;
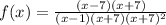 .
.
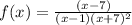 .
.
Let us plug in 5.
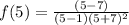 .
.
 .
.
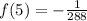 .
.
Let us find the Left Hand Limit;
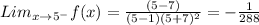 .
.
Now the Right Hand Limit;
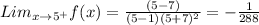 .
.
Since the One-Sided Limits exist and are equal;
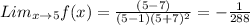 .
.
We have shown that;
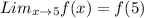 .
.
This is the definition of continuity.
Hence f(x) is continuous at x=5