Answer:
The coordinates of the focus of the parabola are (-6,6)
Explanation:
we know that
The equation of a vertical parabola in vertex form is equal to
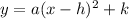
where
(h,k) is the vertex
(h,k+(1/4a)) is the focus
in this problem we have
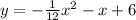
Convert to vertex form
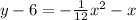
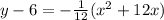
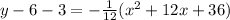
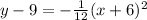
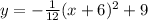 ------> equation in vertex form
------> equation in vertex form
The vertex is the point (-6,9)
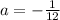
The focus is (h,k+(1/4a)) ------> (-6,9+(1/4(-1/12))-----> (-6,9-3)----> (-6,6)