Answer:
The answer is tanФ = sinФ/cosФ ⇒ the second answer
Explanation:
∵ tanx = sinx/cosx , ∵ cotx = cosx/sinx
∵ tan(π/2 - x) =
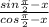
∵ sin(π/2 - x) = cosx ⇒ complementary angles (sum of them = π/2)
∵ cos(π/2 - x) = sinx
∴ tan(π/2 - x) =
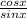 = cotx
= cotx
∴ The identity is tanФ = sinФ/cosФ