Question

Sam drops a ball from a height of 144 feet. How long will it take for the ball

to hit the ground? Ignore the air resistance.

Answer 1

3 seconds for the ball to hit the ground.

Explanation:

To calculate how long it will take for an object to drop(with no force of velocity), use
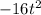`-16t^(2)` and 144 will be our initial height, so we use the equation:

`f(x) = -16t^(2) + 144`

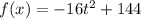
Now, lets simplify this equation. We have a GCF (greatest common factor) of -16, which goes into 144, 9 times. Your simplified equation will look like this.

`f(x) = -16(t^(2) - 9)`

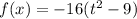
When we have two squares in a group of parentheses, we must simplify that. Therefore, we use the sum and difference pattern. The sum and difference pattern requires a -3 and 3, because two positives and/or two negatives would not result in a -9, so we must use one positive, and one negative. Therefore, we keep the GCF of -16, simplify
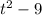`t^(2) -9`, to get a final equation of:

`f(x) = -16(t-3)(t+3)`

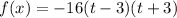
Now, we solve for t to see how long it will take for the ball to reach the ground with no added velocity.

`t=-3,3`

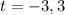
Time can never be negative, when we are talking about a present-time situation. Therefore, we can not have -3 as an answer, and we have 3 as a final answer. It will take 3 seconds for the ball to reach the ground.