Answer:
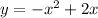
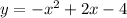
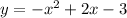
Explanation:
we know that
The equation of a vertical parabola in vertex form is equal to
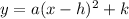
where
(h,k) is the vertex
The axis of symmetry is equal to the x-coordinate of the vertex
so
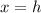
If a> 0 then the parabola open upward (vertex is a minimum)
If a< 0 then the parabola open downward (vertex is a maximum)
In this problem we have
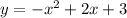
The vertex is the point
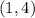 ------> observing the graph
------> observing the graph
The axis of symmetry is

If the graph of this function is shifted downwards and the axis of symmetry remains x=1
then
The x-coordinate of the vertex of the new graph must be equal to 1
The y-coordinate of the vertex of the new graph must be less than 4
The parabola of the new graph open downward
therefore
Verify each case
case a)
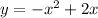
Convert to vertex form
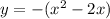
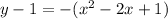
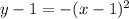
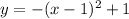
The vertex is (1,1)
therefore
The function could be the equation of the new graph
case b)
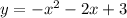
Convert to vertex form
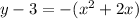
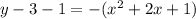
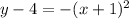
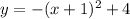
The vertex is (-1,4)
therefore
The function cannot be the equation of the new graph
case c)
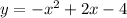
Convert to vertex form
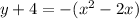
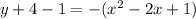
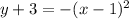
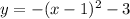
The vertex is (1,-3)
therefore
The function could be the equation of the new graph
case d)
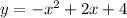
Convert to vertex form
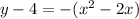
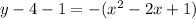
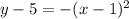
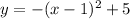
The vertex is (1,5)
therefore
The function cannot be the equation of the new graph
case e)
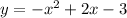
Convert to vertex form
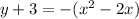

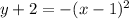

The vertex is (1,-2)
therefore
The function could be the equation of the new graph