Answer:
Choice D is correct.
Explanation:
We have given the sides of triangle:
a =4, b=6, and c =8.
We have to find the area of a triangle.
The formula for the area of triangle is given by:

We have to find the valye of p:
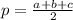
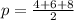
p= 9 units
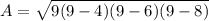
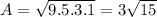
A ≈ 11 .6 units² is the area of triangle.