Answer:
(D) Add 8x to both sides of the inequality.
Explanation:
The given inequality is:
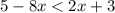
Upon solving the above inequality, we get
Step 1. Subtract 3 from both sides of the inequality.
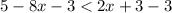
⇒
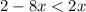
Step 2. Add 8x to both sides of the inequality.

⇒

Step 3. Divide both sides of the inequality by the coefficient of x that is 10.
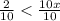
⇒
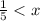
which is the required solved form of the given inequality.
Thus, option D is correct.