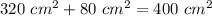Question

A glass paperweight has a composite shape: a square pyramid fitting exacty on top of an 8 centimeter cube. The pyramid has a height of 3 cm. Each triangular face has a height of 5 centimeters.

what is the volume of the paperweight?
what is the total surface area of the paperweight?​

Answer 1

Part 1) The volume of the paperweight is
`576\ cm^(3)`

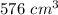
Part 2) The total surface area of the paperweight is
`400\ cm^(2)`

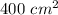
Explanation:

Part 1) what is the volume of the paperweight?

we know that

The volume of the paperweight is equal to the volume of the square pyramid plus the volume of the cube

step 1

Find the volume of the pyramid

The volume of the pyramid is equal to

`V=(1)/(3)BH`

where

B is the area of the square base

H is the height of the pyramid

`B=8^(2)=64\ cm^(2)`

`H=3\ cm`

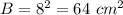
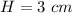
substitute

`V=(1)/(3)(64)(3)=64\ cm^(3)`

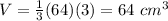
step 2

Find the volume of the cube

The volume of the cube is equal to

`V=b^(3)`

`V=8^(3)=512\ cm^(3)`

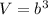
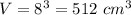
step 3

Find the volume of the paperweight

`64\ cm^(3)+512\ cm^(3)=576\ cm^(3)`

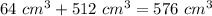
Part 2) what is the total surface area of the paperweight?​

we know that

The total surface area of the paperweight is equal to the surface area of 5 faces of the cube plus the lateral area of the pyramid

step 1

Find the surface area of 5 faces of the cube

`SA=5b^(2)`

`SA=5(8^(2))=320\ cm^(2)`

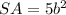
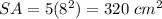
step 2

Find the lateral area of the pyramid

`LA=4[(1)/(2)bh]`

`LA=4[(1)/(2)(8)(5)]=80\ cm^(2)`

step 3

Find the total surface area of the paperweight

`320\ cm^(2)+80\ cm^(2)=400\ cm^(2)`