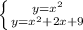Answer:
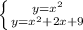
Explanation:
1. As you can see,
 is equal to the other quadratic equation
is equal to the other quadratic equation
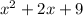 .
.
2. Then, this would the same as write the quadratic equations as following:
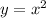
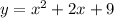
3. And then set them equal to each other, as you can see below:
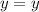
Substituting, you obtain:
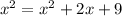
3. Keeping the above on mind, you can set up the given equations as a system of equations as folllowing: