Answer:
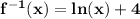
Explanation:
Find the inverse by swapping the x's and y's and then solving for y.

***************************************************************************
Answer:
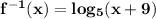
Explanation:
Find the inverse by swapping the x's and y's and then solving for y.

***************************************************************************
Answer:
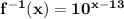
Explanation:
Find the inverse by swapping the x's and y's and then solving for y.
