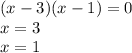Question

What are the roots of the following problems:

1.
`F(x) = (8-x)/(x^(2) -4)`
2.
`F(x) = (x^(2)+4x+8 )/(5x)`
3.
`F(X) = ((X-3)(X-1))/((X+3))`

Answer 1

1. x=8

2. -2+2i and x=-2-2i

3. x=3 and x=1

Explanation:

The denominator of the functions given in the problem cannot be zero, because it is not defined, therefore, you must factorize the numerator to find the roots, as you can see below:

1.
`F(x)=(8-x)/(x^(2)-4)`

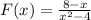
You don't need to factorize the numerator, the root is:

`8-x=0\\-x=-8\\x=8`

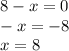
The root is 8.

2. Apply the quadratic formula:

`x=\frac{-b+/-\sqrt{b^(2)-4ac}}{2a}\\\\a=1\\b=4\\c=8\\\\x=\frac{-4+/-\sqrt{4^(2)-4(1)(8)}}{2(1)}`

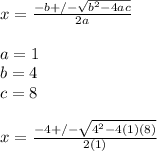
The roots are:

`x=-2+2i\\x=-2-2i`

3. The roots are:

`(x-3)(x-1)=0\\x=3\\x=1`