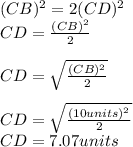Answer: 7.07 units.
Explanation:
You can draw the figure shown attached, where "d" is the diameter of the circle (
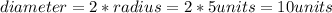 ).
).
The measure of the diagonal CB is equal to diameter of the circle and divides the square into two equal right triangles.
Then, you choose any of the triangles and apply the pythagorean theorem to calculate the side lenght of the square:
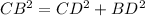
Since it is a square, the sides are equal, then CD=BD. Therefore you can solve for CD as following: