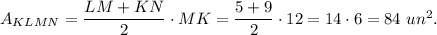Question

Given:

MK
⊥
LM
,
MK
⊥
KN
MN=13, KL=15, LM-KN=4
Find: Area of KLMN.

Answer 1

84 square units.

Explanation:

If LM - KN = 4, then denote KN = x and LM = x+4.

1. Consider right triangle KLM. By the Pythagorean theorem,

`KL^2 =ML^2+MK^2,\\ \\15^2=(x+4)^2+MK^2.`

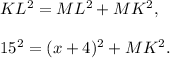
2. Consider right triangle KMN. By the Pythagorean theorem,

`MN^2 =NK^2+MK^2,\\ \\13^2=x^2+MK^2.`

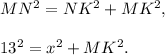
Subtract these two equations:

`15^2-13^2=(x+4)^2-x^2,\\ \\225-169=x^2+8x+16-x^2,\\ \\56=8x+16,\\ \\8x=56-16,\\ \\8x=40,\\ \\x=5\ un.`

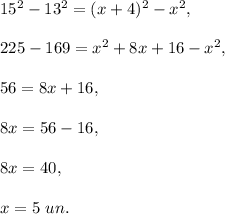
Then

`13^2=5^2+MK^2,\\ \\MK^2=169-25,\\ \\MK^2=144,\\ \\MK=12\ un.`

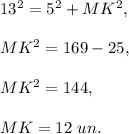
The area of KLMN is

`A_(KLMN)=(LM+KN)/(2)\cdot MK=(5+9)/(2)\cdot 12=14\cdot 6=84\ un^2.`