Question

Find the domain of the function f(t)=√t +3√t

Answer 1

`\mathrm{Domain\:of\:}\:4√(t)\::\quad \begin{bmatrix}\mathrm{Solution:}\:&\:t\ge \:0\:\\ \:\mathrm{Interval\:Notation:}&\:[0,\:\infty \:)\end{bmatrix}`

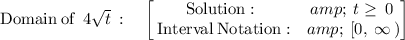
The graph is also attached below.

Explanation:

Given the expression

`f\left(t\right)=√(t)\:+3√(t)`

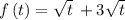
We know that the domain of a function is the set of inputs or argument values for which the function is real and defined.

We know that we can not have a negative value of 't' inside the radicals because if we put any negative number inside the radical expression, it would make the function undefined.

In other words, the value of t ≥ 0.

Therefore, the function domain is:

`\mathrm{Domain\:of\:}\:4√(t)\::\quad \begin{bmatrix}\mathrm{Solution:}\:&\:t\ge \:0\:\\ \:\mathrm{Interval\:Notation:}&\:[0,\:\infty \:)\end{bmatrix}`

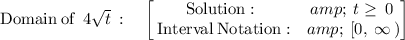
The graph is also attached below.