Question

Show that: (3x+7)^2-84x=(3x -7)^2

Answer 1

Expand the left side than factor

Explanation:

So first expanding the left side gets us
`9x^(2)+ 42x+49-84x=9x^2-42x+49`.

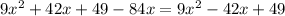Now we factor, you can do it how you like, completeing the square, quadratic equation, you can even use the trick where you split the b term (-42) into two numbers that add up to b and multiply to a*c (9*49=441). I'm going to do the latter.

`9x^(2) -42x+49\\(9x^2-21x)+(-21x+49)\\3x(3x-7)-7(3x-7)\\(3x-7)(3x-7)\\(3x-7)^2`

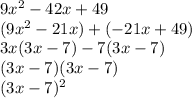
let me know if you need more of an explanation

Answer 2

(3x+7)^2
1st step difference of two squares
So it’s: (3x+7) (3x-7)
So when you expand the brackets it’s the picture above ☝️
So you factorise 9x^ 2 - 49
When you factorise you get (3x-7)(3x-7) or (3x-7) ^2.

Hope this helps.