Answer: The expression is correct
Step-by-step explanation:
We have the following expression:

Where:
Pressure:
 in units of Pascal (
in units of Pascal (
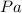 )
)
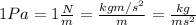
Density:
 in units of
in units of
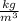
Velocity:
 in units of
in units of
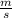
Acceleration due to gravity:
 in units of
in units of
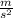
Height:
 in units of
in units of

Knowing this, let's begin with the dimensional analysis:
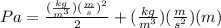
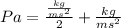
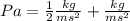
Remembering
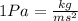 , we are able to know this expression is correct.
, we are able to know this expression is correct.