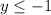Question

What is the range of the function y = -x ^2 + 1?

y ≤ -1
y ≥ -1
y ≤ 1
y ≥ 1

Answer 1

`y \leqslant - 1`

Answer 2

`y\leq -1`

Explanation:

`y = -x ^2 + 1`

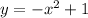
Range is the set of y values for which the function is defined

To find out the range we look at the value of k in the vertex

`y = -x ^2 + 1`

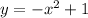
General vertex form is :
`y=a(x-h)^2+k`

where (h,k) is the vertex that is maximum when a is negative

From the given equation the value of k= -1

The graph reaches the maximum value at y=-1

So range is
`y\leq -1`