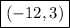Question

Solve for x. Answer in Interval Notation using Grouping Symbols.
x^2+9x<36

Answer 1

`\boxed{(-12,3)}`

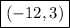
Explanation:

First of all, you must manage this inequality as follows:

`x^2+9x-36<0`

So the roots of the polynomial are:

`x=-12 \ and \ x=3`

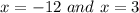
So we can write the inequality as follows:

`(x-3)(x+12)<0`

-12 3

x-3 - - - + +

_________________________

x+12 - - + + +

_________________________

+ + - + +

As you can see from this table, the solution of the inequality in Interval Notation using Grouping Symbols is:

`\boxed{(-12,3)}`

Answer 2

`-12<x<3`

In interval notation: (-12,3)

Explanation:

To solve the expression shown in the problem you must:

- Subtract 36 from both sides, then:

`x^(2)+9x-36<36-36\\x^(2)+9x-36<0`

- Now you must find two number whose sum is 9 and whose produt is 36. These would be -3 and 12. Then, you have:

`(x-3)(x+12)<0`

- Therefore the result is:

`-12<x<3`

In interval notation:

(-12,3)