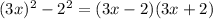Answer:

Explanation:
The given expression is

We can write
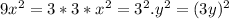 and 4 can be written as square of 2. 4 =
and 4 can be written as square of 2. 4 =
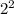
Therefore, we can write

Now we can factor it out.
We are asked to rewrite the expression.
Therefore, the answer is

Let me factor this expression for your reference.